Tefa's universal online electronics calculator

Add unit prefix as a suffix to the number, for example: 1M.
This calculator will automatically add unit prefixes where appropriate. They will be added as a suffix to the calculated value. For example, 0.0012 V (1.2 mV) may be displayed as 1.2 mV, 1.2mV or 1.2m [V] depending on output field format.

Supported unit prefixes:

f	p	n	u	m	c		k	M	G	T	P
femto	pico	nano	micro	milli	centi	(none)	kilo	mega	giga	tera	peta
10^-15	10^-12	10^-9	10^-6	10^-3	10^-2	10⁰	10³	10⁶	10⁹	10¹²	10¹⁵

For squared quantities (for example areas), only the following suffixes are supported: u, m, c, k, M
For convenience, u is used instead of μ.

Version 0.99b-WIP (20220726). Using KaTeX 0.11.1 for equations. This tool is provided without any warranty. Use at your own risk.

Ohm's law

Enter two quantities, the third one will be calculated
$R = \dfrac{V}{I}$

Power (for DC circuits)

Enter two quantities, the third one will be calculated
$P = V \cdot I$

Power (for AC circuits)

Enter two quantities, the third one will be calculated
$P = V \cdot I \cdot \mathrm{cos}(\phi)$
$Q = V \cdot I \cdot \mathrm{cos}(\phi)$
$ |S| = V_{rms} \cdot I_{rms}$

E6/E12/E24 series (IEC 60063 standard)

LED resistor calculator

$R = \dfrac{V_{in}-V_{LED}}{I_{LED}}$

Capacitance, 3 digit code conversion

Enter either capacitance or code, the other value will be auto-calculated
Allowable range: 10pF to 99mF (although capacitors bigger than 10uF usually aren't marked this way)

Tolerance letter	B	C	D	F	G	J	K	M	Z
Tolerance value	±0.1pF	±0.25pF	±0.5pF	±1%	±2%	±5%	±10%	±20%	+80, -20%

Capacitor reactance

Enter two quantities, the third one will be calculated
$X_C = \dfrac{1}{2 \cdot \mathrm{\pi} \cdot f \cdot C}$

Inductor reactance

Enter two quantities, the third one will be calculated
$X_L = 2 \cdot \mathrm{\pi} \cdot f \cdot L$

RLC circuit impedance

$X_L = 2 \cdot \mathrm{\pi} \cdot f \cdot L$
$X_C = \dfrac{1}{2 \cdot \mathrm{\pi} \cdot f \cdot C}$
Serial:
$Z = R + j \cdot 2 \cdot \mathrm{\pi} \cdot f \cdot L - \dfrac{j}{2 \cdot \mathrm{\pi} \cdot f \cdot C}$
$|Z| = \sqrt{R^2+(X_L-X_C)^2}$
If $X_L > X_C$, then $\varphi_i = -\mathrm{arccos} (\dfrac{R}{|Z|})$
If $X_L < X_C$, then $\varphi_i = \mathrm{arccos} (\dfrac{R}{|Z|})$
Parallel:
$|Z| = \dfrac{1}{\sqrt{\frac{1}{R^2} + (\frac{1}{X_L}-\frac{1}{X_C})^2}}$
$\varphi_i = -\mathrm{arctan} (\dfrac{R}{\frac{1}{\frac{1}{X_L} - \frac{1}{X_C}}})$

Resonant frequency

Enter two quantities, the third one will be calculated.
$f_r = \dfrac{1}{2 \cdot \mathrm{\pi} \cdot \sqrt{ L \cdot C}}$

Critical damping (aperiodic) resistance for RLC circuit, LC characteristic impedance

Input quantities:
$Q < 0.5$ ($Q=\dfrac{R}{Z_0}$ for parallel circuit, $Q=\dfrac{Z_0}{R}$ for series circuit, $Z_0 = \sqrt{\dfrac{L}{C}}$)

Capacitor peak dv/dt, peak current

Enter two quantities, the third one will be calculated.
$I_{max}=C \cdot {\mathrm{max}(\dfrac{\mathrm{d}v(t)}{\mathrm{d}t})}$

Capacitive dropper - average rectified current, sine input

This calculator assumes a sine wave input + a constant DC load voltage. For reasonable accuracy, set the limiting resistor value to ≤1/10 of X_C at the selected frequency.
Using the resistance calculated through the classic X_C calculation to calculate the current gives the RMS current value, not the average rectified value, will give inaccurate current & power (~10% error) with a constant voltage load.
The equation was obtained by integrating the average current (i(t)=C*dv/dt) using a "cut" sine wave according to the voltages, and was verified using LTspice.

$I_{avg}=4 \cdot f \cdot C \cdot (V_{p-in}-V_{load}) = I_{avg} = 4 \cdot f \cdot C \cdot (\sqrt{2} \cdot V_{RMS-in} - V_{load})$

Electrolytic, hybrid & solid polymer capacitor lifespan estimation

This calculator uses the "10-degree rule" (doubling the lifetime with every 10°C temperature drop - compared to the lifetime at the rated max. temperature given the specified ripple current and voltage - k₁=2, k₂=10) for "classic" liquid electrolytic/hybrid capacitors and the "20-degree rule" (10 times the life with a 20°C temperature drop - k₁=10, k₂=20).

The estimation won't be particularly accurate at temperatures under 40°C. Also, the lifespan will be much lower at higher currents than specified, at lower currents, it will be higher - refer to manufacturer normograms/datasheets/app-notes for such cases, or the paragraph below.

Optional input - Alternatively, ΔT_C-norm (core self-heating over ambient temperature at rated current, depends on exact capacitor, can be about 5-20 degrees), the rated RMS current at the specified frequency, and the actual load current can be used to calculate lifespan at different currents.

The equations and results were checked against application notes and datasheets provided by big capacitor manufacturers such as Rubycon, TDK or Capxon and were found to be reasonably accurate and universal. No endorsement of this calculator by any of these companies is implied. This calculator should be used as a reference, for guaranteed values, check data provided by the manufacturer.

$life_{actual} = life_{rated} \cdot {k_{1}^{\Bigl(\dfrac{T_{A-rated}-T_{A-actual}}{k_2}\Bigr)}} \\[1.2em] \textrm {or: } life_{actual} = life_{rated} \cdot {k_{1}^ {\Bigl(\dfrac{T_{A-rated}-T_{A-actual} + \Delta T_{C-norm} \cdot (1 - (\frac{I_{actual}}{I_{rated}})^2) }{k_2}\Bigr) } } $

Sine wave dv/dt (di/dt)

Enter two quantities, the other one will be calculated.
$\mathrm{max} \dfrac{\mathrm{d}v(t)}{\mathrm{d}t} = 2 \cdot \mathrm{\pi} \cdot f \cdot V_m$

Sine wave amplitude ↔ RMS

Enter one quantity, the other one will be calculated.
$V_{pk} = \sqrt{2} \cdot V_{rms}$

Rise time, bandwidth

Select encoding/use, enter one quantity, the other one will be calculated.
Assuming first order system, 3 dB permissible attenuation at max. frequency, 10% to 90% rise time, some rounding is done.
NRZ/RZ = (Non) Return-To-Zero
$t_r = \dfrac{0.35}{BW} \mathrm{(RZ)}, t_r = \dfrac{0.7}{BW} \mathrm{(NRZ)}$

RC low-pass filter

Enter three quantities, the fourth one will be calculated.

RC high-pass filter

Enter three quantities, the fourth one will be calculated.

Power ratio / decibel conversion

Input one quantity, the other one will be calculated.
$\mathrm{ratio (dB)} = 10 \cdot \mathrm{lg(ratio)}$

Voltage ratio / decibel conversion

Enter one quantity, the other one will be calculated.
$\mathrm{ratio (dB)} = 20 \cdot \mathrm{lg(ratio)}$

Power / dBm conversion

Enter one quantity, the other one will be calculated.
$P = 10^{(0.1 \cdot ({P_{dBm}-30}))}$

Inductor current rise

$\mathrm{\Delta}I = \dfrac{V \cdot \mathrm{\Delta} T}{L}$

Toroid inductance/turns

For more complex/universal calculations with more possible parameters, use "Gapped or ungapped inductor/transformer saturation current & inductance".

Enter either inductance or turn count, the other quantity will be automatically calculated.
$L = \dfrac{\mu_r \cdot \mathrm{\mu_0} \cdot N^2 \cdot S}{\mathrm{\pi} \cdot d}$

Inductance/turns

This calculator assumes a reasonably high μ and a closed magnetic circuit.

For more complex/universal calculations with more possible parameters, use "Gapped or ungapped inductor/transformer saturation current & inductance".

Enter four quantities, the remaining one will be automatically calculated.
$L = \dfrac{N^2 \cdot S \cdot \mathrm{\mu_0} \cdot \mathrm{\mu_r}}{l}$

Gapped or ungapped inductor/transformer, inductance and saturation current

For ungapped inductors, leave l₂=0, μ_r2=1. Relative permeability of air is 1.

$R_{m1} = \dfrac{l_{1}}{\mu_0 \cdot \mu_{r1} \cdot S}$, $R_{m2} = \dfrac{l_{2}}{\mu_0 \cdot \mu_{r2} \cdot S}$, $R_{m(tot)} = R_{m1}+R_{m2} \\[0.5em]$ $l_{(tot)} = l_1 + l_2$, $\mu_{eff} = \dfrac{l_{(tot)}}{S \cdot R_{m(tot)}}$ $\\[0.5em]$ $L = \dfrac{N^2}{R_{m(tot)}}$, $I_{sat} = \dfrac{l_{(tot)} \cdot B_{max}}{N \cdot \mu_{eff}}$ $\\[0.5em]$ $F_m = N \cdot I$, $\Phi=\dfrac{F_m}{R_{m(tot)}}=B \cdot S$, $L = \dfrac{\Phi}{I}$, $B = \mu \cdot H$, $H = \dfrac{N \cdot I}{l}$ $\\[0.5em]$

Capacitor voltage rise

$\mathrm{\Delta}V = \dfrac{I \cdot \mathrm{\Delta} T}{C}$

Capacitance

Enter three quantities, the other one will be calculated.
$C = \dfrac{S \cdot \epsilon_r \cdot \mathrm{\epsilon_0} }{l}$

Capacitor charge

Enter five quantities, the other one will be automatically calculated
$\tau = R \cdot C$
$t_{total} = \tau \cdot \mathrm{ln} (\dfrac{V_{supply} - V_{initial}}{V_{supply} - V_{final}})$
$V_{final} = V_{initial} + (V_{supply} - V_{initial}) \cdot (1-e^{-t/\tau})$

Capacitor discharge

Enter four quantities, the other one will be automatically calculated
$\tau = R \cdot C$
$V_{final} = V_{initial} \cdot (1-e^{-t/\tau})$

Capacitor stored energy

Enter two quantities, the third one will be automatically calculated
$E = 0.5 \cdot C \cdot V^2$

ESR ↔ tan δ

Enter the frequency, capacitance and either ESR or tan δ
$ESR = X_C \cdot \mathrm{tan}( \delta)$

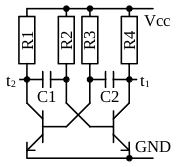
Two transistor astable multivibrator

$\tau_1 = R_2 \cdot C_1$
$\tau_2 = R_3 \cdot C_2$
$t_1 = \tau_1 \cdot \mathrm{ln} (\dfrac{2 V_{CC}}{V_{CC}-V_{BE_{sat}}})$
$t_2 = \tau_1 \cdot \mathrm{ln} (\dfrac{2 V_{CC}}{V_{CC}-V_{BE_{sat}}})$
$f=\dfrac{1}{t_1 + t_2}$

Astable 555 frequency/duty cycle

A duty cycle lower than 50% can be achieved by connecting a diode in parallel to R2.
$V_{ctrl}$ $=$ Control voltage $(\dfrac{\% \mathrm{~of~} V_{CC}}{100})$
No diode parallel to R2: $T_{low} = \mathrm{ln}(2) \cdot R_2 \cdot C$
No diode parallel to R2: $T_{high} = (\mathrm{ln}(\dfrac{1-0.5\cdot {V_{ctrl}}}{1-V_{ctrl}}) \cdot (R1+R2) \cdot C$
Diode parallel to R2: $T_{high} = (\mathrm{ln}(\dfrac{1-0.5\cdot {V_{ctrl}}}{1-V_{ctrl}}) \cdot R1 \cdot C$ (diode drop is neglected)
$T = T_{low} + T_{high}$
$f = \dfrac{1}{T}$
$\mathrm{Duty} (\%) = 100\cdot \dfrac{T_{high}}{T}$

Monostable 555 period

$V_{ctrl}$ $=$ Control voltage $(\dfrac{\% \mathrm{~of~} V_{CC}}{100})$
$T = -\mathrm{ln}(1-V_{ctrl}) \cdot R \cdot C$

IR(S)2153(1)(D) frequency

$f \approx \dfrac{1}{1.4 \cdot (R_t+75) \cdot C_t}$

UC3842, UC3843, UC3844, UC3845 frequency

The result may not be accurate if the timing resistor is lower than 5kΩ
$f_{osc} \approx \dfrac{1.8}{R_t \cdot C_t}$

TL494/KA7500 frequency

$f_{osc} \approx \dfrac{1}{R_t \cdot C_t}$

Voltage regulator feedback

Enter three quantities, the other one will be auto-calculated
$V_{out} = V_{ref} \cdot (\dfrac{R2}{R1}+1)$

Chip	Voltage
LM317T	1.25V
MC34063	1.25V
LM2576-ADJ	1.23V
LM2596-ADJ	1.23V
UC384x (V_FB)	2.5V

MOSFET, IGBT, diode switching loss calculator, SEMIKRON AN1403 method

Calculate conduction loss separately (approximately I_RMS*resistance for FETs, or I_AVG for diodes and IGBTs). Gate drive loss is neglected.
The "scaling factor" K_S is not included in the Semikron PDF. According to simulations, if a MOSFET has a certain switching loss with certain gate drive resistance (external+internal gate resistance) and it is doubled, the loss will be also roughly doubled (Ks≈2). The MOSFET coefficients also aren't present in the original PDF and were determined empirically through simulations. Switch and diode losses must be calculated separately.
Calculate turn-on and turn-off losses separately and add the results. Diode turn-on losses are usually neglectable compared to conduction and turn-off.
$P_{sw} = f \cdot E_{ref} \cdot (\dfrac{I}{I_{ref}})^{K_I} \cdot (\dfrac{V}{V_{ref}})^{K_V} \cdot (1 + K_T \cdot (T-T_{ref})) \cdot K_S$

MOSFET switching loss estimation

Calculate conduction loss separately (approximately I_RMS*resistance for FETs, or I_AVG for diodes and IGBTs).
Switch and diode (internal diode - if it conducts) losses must be also calculated separately.
Don't forget to add prefixes, times are usually in nanoseconds.
The gate resistance effect (t_r, t_f depend on R_g) calculation is usable only if the gate drive voltage is close to the reference.
If only a light load is switched at a high frequency, it might be a good idea to add the D-S capacitance discharge loss. However, this capacitance might also reduce turn-off loss.
The coefficients were determined theoretically by linearizing the waveform and integrating instantaneous power through the switching times while rising/falling. Select "Custom" in dropdown menus to use custom Kl.
$K_g = \dfrac{R_{g\_{int}}+R_{g\_{ext}}}{R_{g\_{int}}+R_{{g\_{ext}}\_{ref}}}$
$E_{cap} = 0.5 \cdot C_{oss} \cdot {V^2_{ds\_{off}}}$
${E_{sw}}_{on} = K_c \cdot K_g \cdot K_l \cdot t_r \cdot {V_{ds\_on}} \cdot {I_{d\_on}}$
${E_{sw}}_{off} = K_c \cdot K_g \cdot K_l \cdot t_f \cdot {V_{ds\_off}} \cdot {I_{d\_off}}$
$P_{sw} = f*({E_{sw\_on}}+{E_{sw\_off}}+E_{cap})$

Switching frequency	Hz
Reference rise time	s
Reference fall time	s
Turn-on drain-source voltage	V
Turn-on drain current	A
Turn-off drain-source voltage	V
Turn-off drain current	A
Consider gate resistor:
External gate resistance	Ω
Reference ext. gate resistance	Ω
Internal gate resistance	Ω
Consider Cds:
Drain-source capacitance	F
Turn-on load:
Turn-off load:
Custom Kl coefficient, turn-on
Custom Kl coefficient, turn-off
Custom E_sw scaling factor K_C:
Power dissipation:	--- [W]

MOSFET/IGBT gate drive loss

$P_{gd} = f \cdot V_{gs\_s} \cdot Q_g$

MOSFET, IGBT, diode, resistor conduction loss calculator

Enter only quantities related to the waveform and part type
This function is quite complex and not well tested yet, implemented only based on theory with few simulations, USE AT YOUR OWN RISK.
For simplicity, constant voltage drop + already rectified signal is assumed for diodes, constant resistance is assumed for MOSFETs.
${P_{D,IGBT}} \approx V_{drop} \cdot I_{ARV}$
$P_{MOSFET} \approx R \cdot I^2_{RMS}$
Table
Multiply RMS value of sine/triangle by sqrt(2) to get RMS value of half-rectified sine/triangle

Waveform	$I_{RMS}$	$I_{ARV}$
Sine	$0.7071 \cdot I_m$	$0.6366 \cdot I_m$
Triangle	$0.5774 \cdot I_m$	$0.5 \cdot I_m$
Square, D=0 to 1	$\sqrt{D \cdot I_{high}^2 +(1-D)\cdot I_{low}^2}$	$D \cdot I_{high} \\+ (1-D) \cdot I_{low}$

Part type:
Waveform:
Rectangular wave, low current:	A
Rectangular wave, high current:	A
Rectangular wave, duty cycle:	%
Sine/half-sine current amplitude:	A
Triangle/half-triangle current amplitude:	A
Custom RMS current:	A
Custom average rectified current:	A
MOSFET on-state/resistor resistance:	Ω
IGBT/Diode voltage drop:	V
Power dissipation:	--- [W]

Hide feature list Show feature list

Function list:

basic calculations (DC power, AC power, LED resistor, Ohm's law, E6/E12/E24 series selector)
capacitor reactance, inductor reactance, RLC impedance, aperiodicity, resonant frequency calculation
capacitor dv/dt, maximum current calculation, tan delta to ESR converter
rise time ↔ bandwidth calculator
decibel to ratio conversions
toroid inductance calculator
capacitor energy and voltage rise
multivibrator, 555, TL494, UC384x frequency calculator
MOSFET, IGBT, diode switching and conduction loss calculator
capacitive dropper current & power calculator
ungapped & gapped inductor/transformer calculator, saturation current and inductance calculation
capacitor (electrolytic, polymer, hybrid) lifespan calculator
MOSFET/IGBT gate drive circuit power calculator
voltage regulator resistive divider calculator

Input quantities:
Voltage	V
Current	A
Phase angle
Output quantities:
Real (active) power	W
Reactive power	var
Apparent power	VA

Input quantities:
Value
Series:
Output quantities:
Closest lower or equal match
Closest higher or equal match
Closest match

Input quantities:
Desired current	A
Input voltage	V
LED voltage	V
Resistor series:
Output quantities:
Calculated resistance	--- [Ω]
Calculated dissipation	--- [W]
Nearest bigger resistor:	--- [Ω]
New LED current*:	--- [A]
* with nearest bigger resistor

Input quantities:
Resistance	Ω
Inductance	H
Capacitance	F
Frequency	Hz
Type:
Output quantities:
Capacitor reactance	--- [Ω]
Inductor reactance	--- [Ω]
Impedance	--- [Ω]
Imaginary impedance part	--- [Ω]
Phase shift (I vs V)	--- [rad]
Phase shift (I vs V)	--- [°]

Inductance	H
Capacitance	F
Type:
Result:
Damping resistance:	--- [Ω]
Z₀:	--- [Ω]

Input quantities:
Rated temperature	°C
Rated lifespan	hours
Actual temperature	°C
Capacitor type:
Optional input quantities:
Custom coefficient k₁
Custom coefficient k₂	°C
Custom ΔT_C-norm, I_rated, I_actual
Core self-heating at rated current	°C
Rated current at rated temperature	A
Actual current	A
Output quantities:
Expected lifetime	--- [hours] (--- [days])

Encoding/use (RZ/NRZ/analog):
Rise time	s
Bandwidth/max. freq.:	Hz/Baud

Input/output quantities:
Resistance	Ω
Capacitance	F
Frequency	Hz
Attenuation	dB
Output quantities:
Phase angle	°

Input quantities:
Permeability
Permeability
Outer diameter	m
Inner diameter	m
Height	m
Cross section	(circular cross-section is calculated from the diameters)
Input/output quantities:
Inductance	H
Turns

Input/output quantities:
Rel. permeability
Turns
Cross section	m²
Magnetic circuit length	m
Inductance	H

Input quantities:
Length 1 (l₁)	m
Rel. permeability 1 (μ_r1)
Length 2 (l₂)	m
Rel. permeability 2 (μ_r2)
Max. flux density	T
Cross section	m²
Turn count
Results:
Inductance:	0 [H]
Max. (saturation) current:	0 [A]
Total length:	0 [m]
Effective rel. permeability:	0
Max. magnetic flux:	0 [Wb]
Part 1 reluctance:	0 [H^-1]
Part 2 reluctance:	0 [H^-1]

Input quantities:
R2	Ω
R3	Ω
C1	F
C2	F
Voltages:
V_BEsat	V
V_CC	V
Output quantities:
Frequency	--- [Hz]
t₁ HIGH (NPN off) time	--- [s]
t₂ HIGH (NPN off) time	--- [s]

Input quantities:
R1 (VCC to DIS)	Ω
R2 (DIS to THR, TR)	Ω
C	F
Diode parallel to R2
Control voltage	% of V_CC
Output quantities:
Frequency	--- [Hz]
HIGH time	--- [s]
LOW time	--- [s]
Duty cycle	--- [%]

Input quantities:
Resistor:	Ω
Capacitor:	F
Control voltage	% of V_CC
Output quantities:
Period:	--- [s]

Input quantities:
Timing resistor:	Ω
Timing capacitor:	F
Output quantities:
Frequency	--- [Hz]

Code
Capacitance	F

Amplitude	V (A)
dv/dt or di/dt	V/s (A/s)
Frequency	Hz

Amplitude	V (A)
RMS	V (A)

Permittivity
Permittivity
Area	m²
Distance	m
Capacitance	F

R1:	Ω (Reference drop)
R2:	Ω
Reference voltage:	V
Output voltage:	V

Part type:	Select "custom" to adjust Kx
Switching loss (energy) at V_ref, I_ref	J
Reference current	A
Reference voltage	V
Reference temperature:	°C
Current:	A
Voltage:	V
Junction temperature:	°C
Frequency:	Hz
Custom Ki:
Custom Kv:
Custom Kt:
Scaling factor:
Power dissipation:	--- [W]

Frequency:	Hz
Gate voltage swing:	V
Gate charge:	C
Power dissipation:	--- [W]